Binary tree is like linked list where each node connects to at most two other nodes. Binary tree is a good example of a recursive data structure. Binary trees have multiple applications in computer science, including Binary Search Trees (BST), the Heap Sort algorithm, and other search/ sorting algorithms for data.
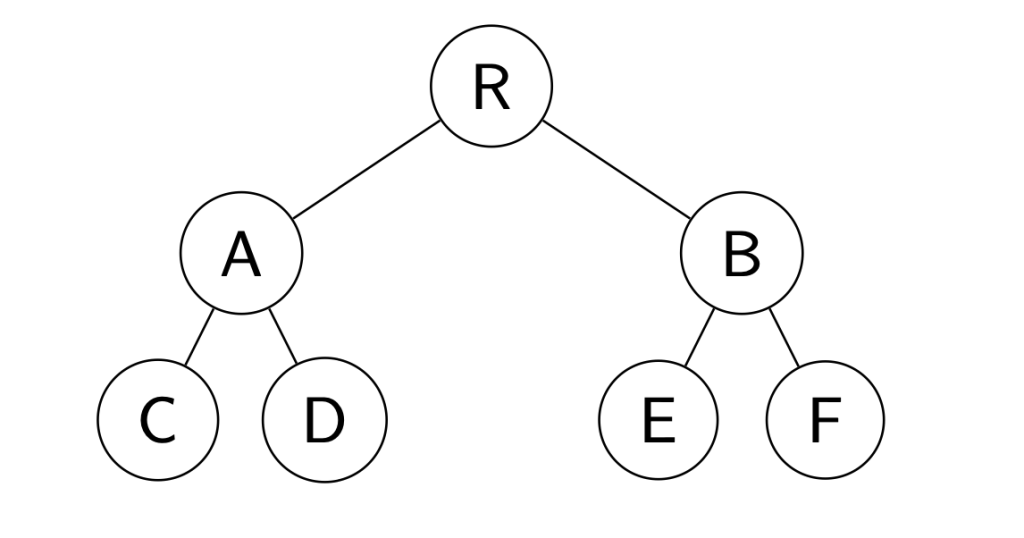
The Binary Tree looks like an upside-down tree. Each element in the Binary Tree is called a node. The node on the top is called the root node, and each node can have at most 2 subtrees. What’s more, the tree can’t contain any loops; otherwise, it will become a graph.
Each node in the tree has to be in a specific level. The root node has the level of 0. The nodes A and B have the level of 1. The nodes C, D, E, and F in this case, have the level of 2. The depth of the tree is the maximum level of the tree.
A common operation on a binary tree is traversal. It’s almost impossible to visit all the nodes by normal loops, since we don’t know exactly how many nodes are there in a tree. Therefore, recursion would be the best way to traversal a tree. The recursive methods for traversal are preorder, inorder, and postorder. The difference of these three methods is the moment that the local root is being visited. In preorder traversal, we visit the local root node first, while in postorder, we visit the local root node in the end.
A Binary Tree can be a Binary Search Tree where in every subtree, the data in the left child is smaller than the root, the data in right child is greater than the root.
Here we will define a Binary Search Tree in Python and implement the three traversal methods.
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def insert(self, new_val):
if new_val < self.data:
if self.left is not None:
self.left.insert(new_val)
else:
self.left = Node(new_val)
else:
if self.right is not None:
self.right.insert(new_val)
else:
self.right = Node(new_val)
def construct_tree(self, L):
for val in L:
self.insert(val)
def preorder(self):
print(self.data, end=", ")
if self.left is not None:
self.left.preorder()
if self.right is not None:
self.right.preorder()
def inorder(self):
if self.left is not None:
self.left.inorder()
print(self.data, end=", ")
if self.right is not None:
self.right.inorder()
def postorder(self):
if self.left is not None:
self.left.postorder()
if self.right is not None:
self.right.postorder()
print(self.data, end=", ")Suppose there is a Binary Search Tree like this:
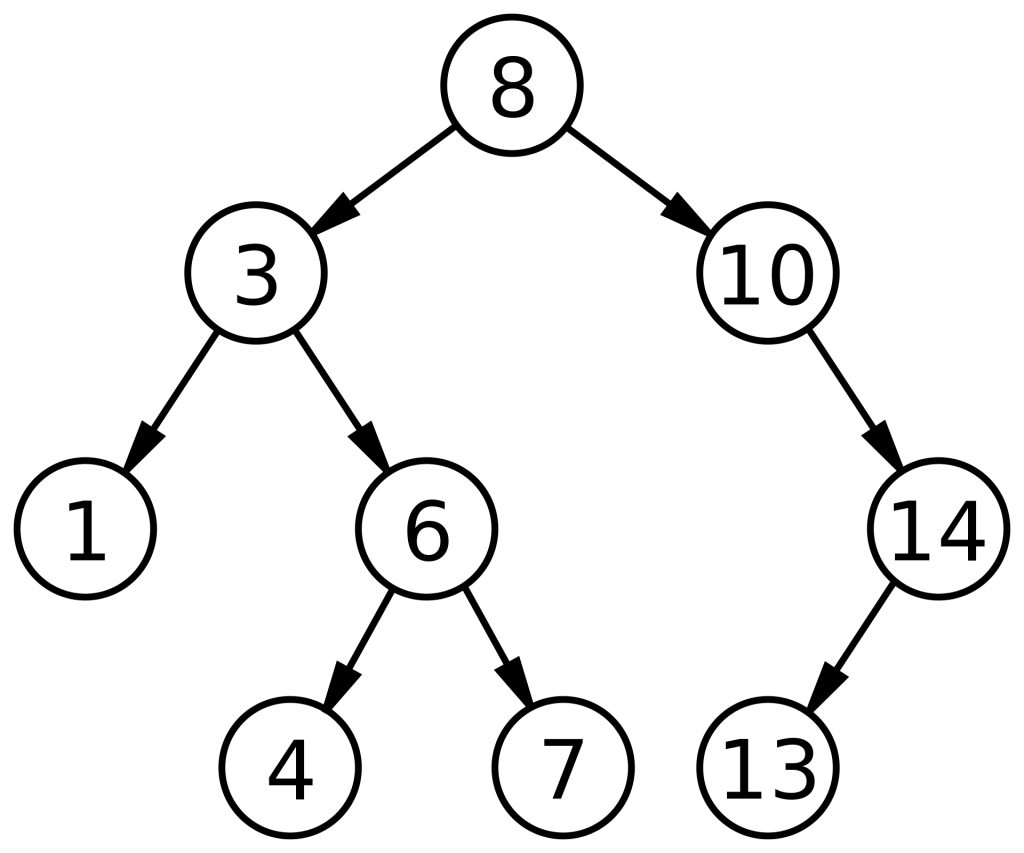
root = Node(8)
root.construct_tree([3, 10, 1, 6, 14, 4, 7, 13])
print("preorder: ")
root.preorder()
print()
print("inorder: ")
root.inorder()
print()
print("postorder: ")
root.postorder()
print()Output:
preorder:
8, 3, 1, 6, 4, 7, 10, 14, 13,
inorder:
1, 3, 4, 6, 7, 8, 10, 13, 14,
postorder:
1, 4, 7, 6, 3, 13, 14, 10, 8, To better understand how recursion works on a binary tree, let’s make two more method: one of them will print the data on the given level (from left to right), the other will get the depth (maximum level) of the binary tree.
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def insert(self, new_val):
if new_val < self.data:
if self.left is not None:
self.left.insert(new_val)
else:
self.left = Node(new_val)
else:
if self.right is not None:
self.right.insert(new_val)
else:
self.right = Node(new_val)
def construct_tree(self, L):
for val in L:
self.insert(val)
# print the data on the given level
def print_lvl(self, lvl):
# base case:
if lvl == 0:
print(self.data)
# recursive steps:
else:
if self.left is not None:
self.left.print_lvl(lvl - 1)
if self.right is not None:
self.right.print_lvl(lvl - 1)
# return the depth of the tree
def get_depth(self):
# base case:
if self.left is None and self.right is None:
return 0
# recursive step:
left = 0
right = 0
if self.left is None:
left = 0
elif self.left is not None:
left = self.left.get_depth() + 1
if self.right is None:
right = 0
elif self.right is not None:
right = self.right.get_depth() + 1
return max(left, right)Suppose the binary tree doesn’t change:
root = BinaryTree.Node(8)
root.construct_tree([3, 10, 1, 6, 14, 4, 7, 13])
print("the data on the level 2: ")
root.print_lvl(2)
print("the depth of the tree: ")
print(root.get_depth())Output:
the data on the level 2:
1
6
14
the depth of the tree:
3